XÂY DỰNG SƠ ĐỒ ĐỘ SÂU VÙNG BIỂN VEN BỜ PHÍA NAM VỊNH NHA TRANG DỰA TRÊN PHƯƠNG PHÁP NỘI SUY NGHỊCH ĐẢO KHOẢNG CÁCH CÓ TRỌNG SỐ

Tóm tắt

CONSTRUCTING THE BATHYMETRIC MAP OF THE SOUTHERN COASTAL AREA OF NHA TRANG BAY BASED ON THE WEIGHTED INVERSE DISTANCE INTERPOLATION METHOD

The bathymetric maps of shallow coastal areas, islands, and sandbanks are considered useful sources of information and serve as a basis for creating maritime safety charts and managing the environmental resources of water bodies. This study uses open-source software (R and QGIS) to evaluate the influence of different ratios between training and validation datasets, while also optimizing the power parameter (p) and the number of neighboring sample points (n) in the IDW interpolation method. The goal is to create a bathymetric map for the southern coastal area of Nha Trang Bay using data from GEBCO_2023 and field survey depth measurements. The results show that increasing the number of training data points and optimizing the parameters p and n reduces the error of the IDW interpolation algorithm. This study indicates that the bathymetry dataset data80 (with a ratio of 80% training and 20% validation), a power parameter of 2, and a number of neighboring sample points of 4 are considered the optimal ratio and parameters, and are used to create a bathymetric map with a resolution of 3 m x 3 m in the study area. The RMSE between the measured and predicted bathymetry data from the IDW interpolation algorithm is 0.597 m. In the southern water area of Nha Trang Bay, the spatial distribution of bathymetry tends to increase from the shore outward.

1. ĐẶT VẤN ĐỀ

          Đo độ sâu liên quan đến việc đo hoặc nghiên cứu độ sâu của thủy vực tại các vùng biển, sông hoặc hồ [1]. Thông tin từ bản đồ độ sâu, hoặc các nghiên cứu về độ sâu của thủy vực có vai trò quan trọng trong nhiều lĩnh vực như hải dương học, nghiên cứu khí hậu, khí tượng học, nghiên cứu địa chất biển, quản lý hàng hải, quản lý bờ biển, giám sát tài nguyên môi trường và thủy sinh vật [1, 2]. Bên cạnh đó, dữ liệu độ sâu cũng được xem là nguồn thông tin rất cần thiết để đạt được kết quả chính xác trong các mô hình thủy động lực học của sông, cửa sông và vùng ven biển [3]. Vì vậy, xây dựng sơ đồ độ sâu tại khu vực nước nông ven bờ, các đảo, các bãi cạn làm cơ sở để lập bản đồ an toàn hàng hải, quản lý tài nguyên môi trường thủy vực là cần thiết phải thực hiện.

        Vịnh Nha Trang có vị trí địa lý ở phía đông của thành phố Nha Trang, được xem là một trong 29 vịnh đẹp của Thế giới. Ngày nay, vịnh Nha Trang thu hút nhiều khách du lịch bởi phong cảnh đẹp và có giá trị cao về đa dạng sinh học, đặc biệt là hệ sinh thái rạn san hô. Thống kê từ nghiên cứu trước đây cho thấy ở khu vực phía Nam vịnh Nha Trang như Hòn Miễu, Hòn Tằm, Hòn Một, Hòn Tre, Hòn Mun tập trung nhiều rạn san hô [4]. Do đó, nghiên cứu này được thực hiện nhằm nội suy độ sâu từ các tập dữ liệu độ sâu sẵn có, tạo nền tảng cung cấp dữ liệu độ sâu để hiệu chỉnh cột nước, góp phần quan trọng trong việc phân tích và giải đoán phân bố không gian của san hô ở khu vực phía Nam vịnh Nha Trang. Bên cạnh đó, sơ đồ độ sâu từ nghiên cứu này còn đóng góp cho an toàn hàng hải, cung cấp thông tin độ sâu cho các nghiên cứu liên quan đến lĩnh vực tài nguyên và môi trường biển.

         Thông thường, độ sâu của thủy vực được đo đạc thông qua các cuộc khảo sát thực địa đo độ sâu bằng thiết bị đo đơn tia hoặc đa tia. Tuy nhiên, kết quả đo đạc độ sâu thực địa không đủ để xây dựng mô hình số địa hình (DEM - Digital Terrain Models) của đáy biển do thiếu độ sâu tại các điểm không được đo đạc [5]. Hiện nay, nhiều phương pháp khác nhau được sử dụng để xây dựng sơ đồ độ sâu, bao gồm các phương pháp nội suy không gian từ dữ liệu độ sâu đo đạc hiện trường, phương pháp dựa trên dữ liệu địa hình, và phương pháp viễn thám. Trong các phương pháp này, nội suy không gian là phổ biến nhất để xây dựng sơ đồ độ sâu [6]. Vì vậy khi xây dựng bản đồ độ sâu, bản đồ DEM đáy biển, các kỹ thuật nội suy không gian được sử dụng để ước tính giá trị độ sâu tại các vị trí không được đo đạc hiện trường [3, 5]. Việc nội suy dữ liệu độ sâu trong thủy văn giúp tiết kiệm chi phí thực địa và nhân công, đồng thời bổ sung dữ liệu hiệu quả mà vẫn đảm bảo tạo ra các sơ đồ độ sâu dạng raster phục vụ cho nhiều mục đích khác nhau.

          Nội suy là một phương pháp toán học được sử dụng để dự đoán các giá trị chưa biết/chưa đo đạc (ví dụ như độ sâu tại vùng biển ven bờ) bằng cách dựa vào các giá trị đã được đo đạc xung quanh [7]. Hiện nay có hơn 40 phương pháp nội suy không gian đã được tổng quan, và nó được chia thành 3 nhóm bao gồm nội suy địa thống kê, nội suy xác định/không thuộc địa thống kê, nội suy kết hợp, và trong đó mỗi phương pháp nội suy ảnh hưởng bởi nhiều yếu tố khác nhau trên tập dữ liệu cần nội suy [6, 8]. Đã có nhiều nghiên cứu sử dụng các phương pháp nội suy không gian khác nhau để xây dựng bản đồ độ sâu của thủy vực. Nghiên cứu [9] đã sử dụng phương pháp nội suy Kriging và nội suy nghịch đảo khoảng cách có trọng số (IDW - Inverse distance weighted) để lập bản đồ độ sâu vùng Yucantan. Nghiên cứu [10] đã sử dụng 7 phương pháp nội suy khác nhau (bao gồm: IDW, RS - Regularized Spline, ST - Spline with Tension, TG - Topogrid, NN - Natural Neighbor, OK - Ordinary Kriging và AK - Ordinary Kriging with Anisotropy) để nội suy độ sâu tại các thủy vực sông khác nhau tại Hoa Kỳ. Nghiên cứu [6] cho thấy phương pháp nội suy địa không gian (OK - Ordinary Kriging) có độ chính xác cao hơn so với phương pháp nội suy khác địa không gian (IDW, LPI - Local Polynomial Interpolation, RBF - Radial Basis Function) khi lập bản đồ độ sâu tại hồ chứa thủy điện Tucuruí (nằm ở Amazon của Brazil). Nghiên cứu [11] đã so sánh 3 phương pháp nội suy IDW, Kriging và TIN (Triangular Irregular Network) khi thực hiện nội suy độ sâu tại đảo Bawean, phía Đông Java. Kết quả cho thấy phương pháp IDW phù hợp nhất và có sai số thấp nhất khi nội suy dữ liệu độ sâu tại vùng nghiên cứu. Nghiên cứu [12] cũng cho thấy khi xây dựng bản đồ độ sâu tại Saldanha Bay (South Africa), phương pháp IDW phù hợp hơn so với phương pháp OK. Kết quả của những nghiên cứu trên cho thấy phương pháp nội suy tối ưu sẽ khác nhau tại mỗi vùng địa lý khác nhau. Hiện nay vẫn chưa có nghiên cứu nào khẳng định phương pháp nội suy nào là tốt nhất cho mọi trường hợp [6]. 

            Trong các phương pháp nội suy phổ biến, IDW được xem là một trong những phương pháp nội suy đơn giản, trực quan, dễ diễn giải kết quả nhưng vẫn đảm bảo độ chính xác và độ tin cậy cần thiết, được tích hợp sẵn trong hầu hết các phần mềm GIS [13]. Trong nghiên cứu này, phương pháp nội suy IDW được lựa chọn sử dụng để xây dựng sơ đồ độ sâu tại vùng biển phía Nam vịnh Nha Trang. Các nghiên cứu trước đây cho thấy phương pháp nội suy IDW ảnh hưởng bởi tham số lũy thừa (p) và số lượng điểm mẫu lân cận (n) được sử dụng [9, 12]. Khi tham số p thấp sẽ làm mượt bề mặt nội suy, và giá trị trọng số cao sẽ đặt nhiều trọng số hơn vào các điểm đã biết gần nhất, khiến bề mặt nội suy ít mượt mà hơn. Bên cạnh đó, việc tăng số điểm mẫu lân cận sẽ làm mượt bề mặt nội suy, trong khi thiếu điểm mẫu lân cận có thể giảm độ chính xác của kết quả và tạo ra hiệu ứng mắt bò (“bull’s-eye”) [12]. Ngoài ra, nghiên cứu [12] cho thấy rằng số lượng điểm dữ liệu đầu vào khác nhau cũng ảnh hưởng đến sai số của phương pháp nội suy IDW; cụ thể, khi sử dụng toàn bộ dữ liệu đầu vào (100%), sai số giảm hơn so với khi chỉ sử dụng hai phần ba (66%) hoặc một phần ba (33%) dữ liệu đầu vào. Do đó, nghiên cứu này được thực hiện với mục đích: (1) đánh giá ảnh hưởng của các tỷ lệ khác nhau giữa tập dữ liệu huấn luyện và tập dữ liệu kiểm định; (2) tối ưu hóa tham số lũy thừa và số lượng điểm mẫu lân cận trong phương pháp nội suy IDW, nhằm xây dựng sơ đồ độ sâu tại khu vực phía Nam vịnh Nha Trang. Kết quả của nghiên cứu này không chỉ gia tăng độ chính xác của phương pháp nội suy IDW mà còn đóng góp vào việc xây dựng các sơ đồ độ sâu chi tiết và tin cậy cho các vùng nước ven bờ, từ đó hỗ trợ hiệu quả trong các ứng dụng quản lý tài nguyên và môi trường biển.

2. DỮ LIỆU VÀ PHƯƠNG PHÁP NGHIÊN CỨU

2.1. Khu vực nghiên cứu

         Nghiên cứu được thực hiện ở phía Nam vịnh Nha Trang, thành phố Nha Trang, tỉnh Khánh Hòa (Hình 1). Nghiên cứu trước đây cho thấy kiến trúc hình thái địa hình đáy biển vịnh Nha Trang rất đa dạng, phức tạp. Khu vực phía Nam vịnh Nha Trang được chia cắt bởi một hệ thống các đảo lớn nhỏ (Hòn Mun, Hòn Tằm, Hòn Một, Hòn Miễu, Hòn Tre), tạo ra một bề mặt đáy biển đặc trưng với nhiều dạng địa hình như lạch sâu và máng trũng ở độ sâu từ 15-20 m nằm xen kẽ giữa các đảo [14]. 

2.2. Dữ liệu

         Dữ liệu độ sâu được đo đạc hiện trường vào tháng 3 và tháng 4 năm 2024 ở vịnh Nha Trang bằng thiết bị đo sâu đơn tia GPSMAP 585 PLUS (GARMIN, Đài Loan: https://www.garmin.com.my/products/onthewater/gpsmap-585-plus/, truy cập ngày 27/7/2024). Tổng cộng 10.535 điểm dữ liệu đo độ sâu (đơn vị: m) được thu thập trong quá trình khảo sát độ sâu tại vùng nghiên cứu (Hình 1). Độ chính xác của các thuật toán nội suy độ sâu phụ thuộc vào mật độ và phân bố dữ liệu đo sâu thực địa [3]. Thuật toán nội suy IDW nhạy với dữ liệu phân cụm và có thể không hoạt động hiệu quả trong điều kiện các điểm đo đạc thực địa không phân bố đều xung quanh các điểm cần ước tính [5]. Do đó, nguồn dữ liệu độ sâu từ mô hình Hải đồ độ sâu tổng quát các đại dương (GEBCO - General Bathymetric Chart of the Oceans) được sử dụng để bổ sung cho các điểm dữ liệu độ sâu đo đạc hiện trường, tránh trường hợp phân cụm dữ liệu độ sâu thực đo.

            Dữ liệu GEBCO_2023 là một mô hình địa hình toàn cầu bao phủ cả đại dương và đất liền, cung cấp dữ liệu độ sâu đo bằng mét trên lưới có độ phân giải 15 giây. Dữ liệu GEBCO_2023 gồm 43.200 hàng và 86.400 cột, tương ứng với 3.732.480.000 điểm dữ liệu. Các giá trị độ sâu được ghi lại tại tâm của mỗi pixel, đại diện cho độ sâu ở tâm của mỗi ô lưới. GEBCO_2023 được công bố vào tháng 4 năm 2023 và là lưới GEBCO thứ năm được phát triển thông qua Dự án Đáy biển 2030 của Quỹ Nippon (Nhật Bản) và GEBCO. Đây là một dự án hợp tác giữa Quỹ Nippon của Nhật Bản và GEBCO, nhằm thu thập tất cả dữ liệu đo độ sâu có sẵn để tạo ra một bản đồ chi tiết về đáy đại dương trên phạm vi toàn cầu (https://www.gebco.net/data_and_products/gridded_bathymetry_data/gebco_2023/, truy cập ngày 27/7/2024). Dữ liệu GEBCO_2023 được truy cập và tải miễn phí tại trang web của GEBCO (https://download.gebco.net/), (truy cập ngày 10/5/2024). Trong bài báo này, tổng cộng 563 điểm dữ liệu (pixel) độ sâu (đơn vị: m) từ bộ dữ liệu của GEBCO_2023 tại vùng nghiên cứu được sử dụng (Hình 1).

           Dữ liệu độ sâu từ bộ dữ liệu GEBCO_2023 được chuyển đổi sang cùng hệ tọa độ với dữ liệu độ sâu đo đạc tại hiện trường, sử dụng hệ tọa độ WGS 84, múi chiếu 49N.

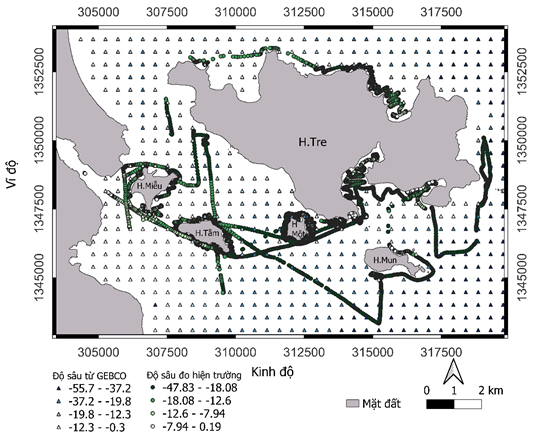
Hình 1. Phân bố của dữ liệu độ sâu thực đo và độ sâu từ mô hình GEBCO_2023 tại vùng nghiên cứu

2.3. Phương pháp nội suy khoảng cách nghịch đảo trọng số và xây dựng sơ đồ độ sâu

        Kỹ thuật nội suy khoảng cách nghịch đảo trọng số xác định giá trị độ sâu cần nội suy bằng cách tính trung bình trọng số khoảng cách của giá trị độ sâu tại các vị trí nằm trong vùng lân cận của điểm cần tính. Mỗi điểm lân cận đều ảnh hưởng đến giá trị cần nội suy, trong đó ảnh hưởng của điểm lân cận giảm dần theo khoảng cách từ điểm lân cận đến điểm cần nội suy [15]. Từ đó cho thấy các điểm mẫu càng cách xa điểm cần nội suy sẽ càng ít ảnh hưởng đến giá trị nội suy, và ngược lại, các điểm mẫu càng gần điểm nội suy thì ảnh hưởng càng lớn đến giá trị nội suy. Giá trị độ sâu cần nội suy tại vị trí x₀, kí hiệu  (x₀) được xác định theo phương trình (1) [8]:

                                                 (1)

Trong đó:

- z (x_i) là giá trị của độ sâu tại vị trí được đo đạc i;

- n là số vị trí lấy mẫu lân cận được sử dụng cho ước tính  (x₀);

- d_i là khoảng cách giữa điểm x₀ và điểm x_i;

- p là tham số lũy thừa.

         Thuật toán nội suy IDW có ưu điểm là tạo ra các bề mặt nội suy mượt mà và tính đến các tham số kích thước, số lượng điểm lấy mẫu và tham số lũy thừa, kiểm soát các điểm lân cận được gán trọng số trên các điểm nội suy. Phương pháp nội suy IDW ảnh hưởng bởi tham số lũy thừa (p) và số lượng điểm mẫu lân cận (n) được sử dụng. Thông thường, việc tìm kiếm giá trị p tối ưu là một quá trình tìm kiếm trên lưới: một khoảng giá trị của p cụ thể được thiết lập tùy ý hoặc dựa trên trực giác của nhà nghiên cứu, sau đó p sẽ lấy tất cả các giá trị trong khoảng đó, với một bước nhảy nhất định được chọn tùy ý [16]. Ứng với giá trị p có sai số thấp nhất trong số các giá trị được tìm kiếm sẽ được lựa chọn để gán cho tham số này. Do đó, việc tối ưu hóa giá trị của tham số lũy thừa (p) và số lượng điểm mẫu lân cận (n) để giảm thiểu sai số của thuật toán nội suy IDW là điều cần thiết.

          Quy trình đánh giá ảnh hưởng của các tỷ lệ khác nhau giữa tập dữ liệu huấn luyện và tập dữ liệu kiểm định; và tối ưu hóa tham số lũy thừa, số lượng điểm mẫu lân cận trong phương pháp nội suy IDW nhằm thành lập sơ đồ độ sâu được trình bày trên Hình 2, thông qua các bước sau:

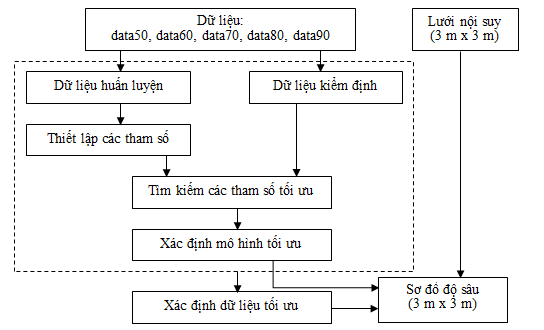
Hình 2. Quy trình xác định tham số tối ưu và dữ liệu tối ưu

            - (1) Xây dựng lưới nội suy và phân chia ngẫu nhiên dữ liệu: Lưới nội suy với độ phân giải 3 m x 3 m được xây dựng để thực hiện phép tính nội suy trên các điểm lưới. Bộ dữ liệu độ sâu đầu vào được chia ngẫu nhiên thành 2 tập dữ liệu: tập huấn luyện và tập kiểm định với các tỷ lệ khác nhau bằng hàm sample trên ngôn ngữ R. Các tập dữ liệu sau khi phân chia bao gồm: data50 (50% huấn luyện: 50% kiểm định), data60 (60% huấn luyện: 40% kiểm định), data70 (70% huấn luyện: 30% kiểm định), data80 (80% huấn luyện: 20% kiểm định), data90 (90% huấn luyện: 10% kiểm định). Tập dữ liệu huấn luyện bao gồm cả giá trị độ sâu đo đạc hiện trường và độ sâu từ mô hình GEBCO, trong khi tập dữ liệu kiểm định chỉ chứa giá trị độ sâu đo đạc hiện trường.

          -  (2) Thiết lập các tham số: Một dãy các giá trị của tham số được thiết lập để thử nghiệm, bao gồm các giá trị cho tham số n dao động từ 2 đến 20 với bước nhảy là 2, và giá trị của tham số p dao động từ 0,5 đến 10 với bước nhảy là 0,5. 

          - (3) Tìm kiếm các tham số (p và n) tối ưu: Vòng lặp với 200 mô hình được sử dụng để xây dựng và đánh giá các mô hình IDW với từng cặp tham số p và n trong lưới đã thiết lập (20 giá trị p x 10 giá trị n). Mỗi lần lặp, một mô hình IDW được xây dựng trên tập dữ liệu huấn luyện với các tham số hiện tại và được sử dụng để dự đoán giá trị trên tập dữ liệu kiểm định. Sai số trung bình toàn phương (RMSE - Root Mean Square Error) được tính toán giữa giá trị độ sâu dự đoán từ mô hình IDW và giá trị độ sâu thực tế trên tập dữ liệu kiểm định. Chỉ số RMSE được sử dụng để đánh giá sai số của thuật toán nội suy IDW. Theo chỉ số này, mô hình nào có RMSE càng thấp thì mức độ phù hợp của mô hình càng cao, chỉ số RMSE được tính toán theo phương trình (2) [17]:

                                    (2)

           Với N là tổng số mẫu quan sát, Y_i là giá trị độ sâu được nội suy tại vị trí i; O_i là giá trị độ sâu được đo đạc (từ bộ dữ liệu kiểm định) tại vị trí i.

          Kiểm định Pearson được sử dụng để đánh giá mối quan hệ tuyến tính giữa độ sâu đo đạc hiện trường và độ sâu được dự báo từ thuật toán nội suy IDW, kiểm định có ý nghĩa thống kê khi P < 0,05 [18].

           - (4) Xác định mô hình tối ưu với cặp tham số p và n tối ưu: Sau khi chạy 200 mô hình khác nhau, giá trị của cặp tham số p và n cho kết quả RMSE thấp nhất được xác định là giá trị tối ưu cho mô hình nội suy IDW, đảm bảo rằng mô hình nội suy có khả năng dự báo chính xác nhất có thể trên dữ liệu thực tế.

           - (5) Xác định dữ liệu tối ưu: Lặp lại các bước từ (1) đến (4) cho từng tập dữ liệu: data50, data60, data70, data80, và data90. Trong số năm tập dữ liệu này, tập dữ liệu nào có giá trị RMSE trung bình thấp nhất sẽ được sử dụng để thực hiện nội suy IDW. Kiểm định one way ANOVA được sử dụng để kiểm tra sự khác biệt về giá trị RMSE giữa các tập dữ liệu [18]. Trong trường hợp có sự khác biệt về giá trị RMSE mang ý nghĩa thống kê, kiểm định Tukey's Honestly Significant Difference (HSD) sẽ được sử dụng để xác định các cặp dữ liệu có sự khác biệt [18]. Trong các kiểm định one way ANOVA và Tukey’s HSD, sự khác biệt được coi là có ý nghĩa thống kê khi P < 0,05.

            - (6) Xây dựng sơ đồ phân bố độ sâu: Dữ liệu tối ưu, mô hình tối ưu được sử dụng để thực hiện phép tính nội suy IDW trên lưới nội suy độ phân giải 3m x 3m. Tập dữ liệu độ sâu sau khi nội suy sẽ được chuyển đổi từ định dạng data frame sang định dạng raster. Phần mềm mã nguồn mở QGIS được sử dụng để xây dựng sơ đồ độ sâu tại phía Nam vịnh Nha Trang với tỷ lệ 1:50.000, hệ quy chiếu WGS 84, múi chiếu 49N từ dữ liệu raster độ sâu.

           Gói gstat trên ngôn ngữ thống kê mã nguồn mở R được sử dụng để thực hiện phép tính nội suy IDW. Theo đó, các tham số trong phương trình (1) trên gói gstat được giữ nguyên theo mặc định, chỉ điều chỉnh tham số p và n để cải thiện độ chính xác của phương pháp nội suy IDW. Toàn bộ các phép tính, kiểm định thống kê và đồ thị được thực hiện bằng ngôn ngữ R.

3. KẾT QUẢ NGHIÊN CỨU VÀ THẢO LUẬN

         Kết quả nghiên cứu cho thấy, tỷ lệ khác nhau giữa tập dữ liệu huấn luyện và tập dữ liệu kiểm định có ảnh hưởng đáng kể đến độ chính xác của thuật toán nội suy không gian IDW (Bảng 1, Hình 3a). Trong số các tập dữ liệu được sử dụng, tập dữ liệu data80 (80% dữ liệu huấn luyện: 20% dữ liệu kiểm định) và data90 (90% dữ liệu huấn luyện: 10% dữ liệu kiểm định) có sai số thấp nhất với giá trị RMSE trung bình tương ứng đạt 0,597 m và 0,575m (Bảng 1, Hình 3). Trong khi đó, tập dữ liệu data50 có sai số lớn nhất với RMSE trung bình đạt 0,875 m (Bảng 1, Hình 3). Giá trị RMSE của các tập dữ liệu data60 và data70 lần lượt đạt 0,746 m và 0,658 m. Bảng 1 cho thấy rằng các tập dữ liệu đầu vào khác nhau có ảnh hưởng đến sai số của thuật toán nội suy IDW, chênh lệch giá trị RMSE giữa tập dữ liệu data90 và data50 là 0,3 m. Kết quả này cho thấy rằng sử dụng nhiều điểm lấy mẫu (điểm đo sâu) giúp cải thiện sai số của kết quả nội suy IDW, nghĩa là độ chính xác của thuật toán nội suy IDW được cải thiện khi tăng số lượng điểm dữ liệu đầu vào. Nghiên cứu trước đây cũng cho thấy khi thực hiện thuật toán nội suy IDW, tăng số lượng điểm dữ liệu đầu vào giúp giảm sai số của thuật toán nội suy [12].

Bảng 1. Tối ưu tập dữ liệu, tham số lũy thừa và số lượng điểm mẫu lân cận

trong IDW

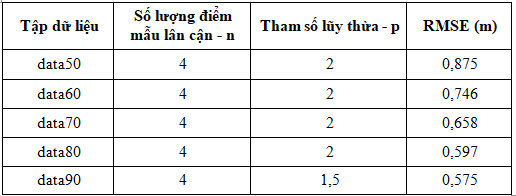
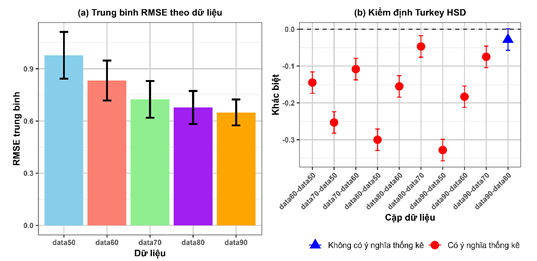
Hình 3. So sánh và kiểm định sự khác biệt RMSE giữa các tập dữ liệu

          Kết quả kiểm định ANOVA cho thấy sự khác biệt về giá trị RMSE giữa các tập dữ liệu có nghĩa thống kê (ANOVA, P < 0,001) (Hình 3b). Sự khác biệt về giá trị RMSE giữa từng cặp dữ liệu hầu hết đều có khác biệt mang ý nghĩa thống kê (Tukey HSD, P < 0,001), ngoại trừ cặp dữ liệu data80-data90 (Tukey’s HSD, P > 0,05) (Hình 3b). Sai số RMSE giữa tập dữ liệu huấn luyện và tập dữ liệu kiểm định trên bộ dữ liệu data90 có giá trị thấp nhất. Tuy nhiên, sự chênh lệch về giá trị RMSE giữa tập data90 và data80 rất nhỏ (0,022 m) và không có khác biệt mang ý nghĩa thống kê. Do đó, tập dữ liệu data80 được sử dụng như tập dữ liệu tối ưu để thực hiện thuật toán nội suy IDW nhằm xây dựng sơ đồ độ sâu tại vùng nghiên cứu. 

        Kết quả tối ưu hóa tham số lũy thừa và số lượng điểm mẫu lân cận trong nội suy IDW được trình bày trong Bảng 1. Trong các tập dữ liệu được sử dụng, số lượng điểm mẫu lân cận tối ưu được sử dụng trong mô hình nội suy IDW là 4. Kết quả nghiên cứu cũng cho thấy hầu hết giá trị của tham số p tối ưu thường đạt 2 ở các tập dữ liệu, trong khi đó ở tập dữ liệu data90, p tối ưu với giá trị 1,5.

         Kết quả ở Hình 3 cho thấy thuật toán nội suy IDW đạt hiệu quả tối ưu nhất ứng với dữ liệu data80, tham số lũy thừa bằng 2 và số lượng điểm mẫu lân cận bằng 4. Nghiên cứu này đã huấn luyện và kiểm định 1000 mô hình nội suy IDW với 200 vòng lặp để tối ưu hóa tham số lũy thừa và số lượng điểm mẫu lân cận, và 5 vòng lặp để tối ưu hóa tập dữ liệu. Kết quả cho thấy tập dữ liệu độ sâu data80 (với tỷ lệ 80% huấn luyện và 20% kiểm định), tham số lũy thừa bằng 2 và số lượng điểm mẫu lân cận bằng 4 là phù hợp nhất để xây dựng sơ đồ độ sâu tại khu vực phía Nam vịnh Nha Trang. Những nghiên cứu trước đây chỉ ra rằng tham số lũy thừa p ảnh hưởng lớn đến độ chính xác của phương pháp nội suy IDW, và lựa chọn mặc định cho tham số p là 2 [8, 19]. Nghiên cứu [20] cho thấy độ chính xác của phương pháp nội suy IDW cao nhất với giá trị p bằng 2 trong số các giá trị p đã sử dụng bao gồm 1; 1,5; 2; 2,5; 3; 3,5. 

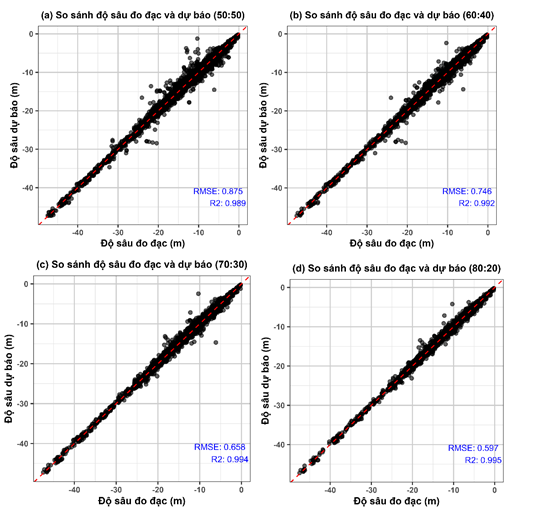
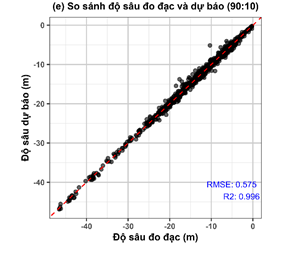
Hình 4. So sánh độ sâu đo đạc và độ sâu dự báo từ mô hình nội suy IDW

với các tập dữ liệu khác nhau

         Hình 4 trình bày mối quan hệ tuyến tính giữa độ sâu đo đạc hiện trường và độ sâu được dự báo từ thuật toán nội suy IDW trên các tập dữ liệu khác nhau (data50 - Hình 4a, data60 - Hình 4b, data70 - Hình 4c, data80 - Hình 4d, data90 - Hình 4e). Kết quả kiểm định cho thấy có mối tương quan mang ý nghĩa thống kê giữa độ sâu đo đạc và độ sâu dự báo từ mô hình IDW (Pearson, P < 0,001) với hệ số R² lớn hơn 0,98 ở tất cả các tập dữ liệu được sử dụng.

          Sau khi xác định được tập dữ liệu tối ưu và các tham số lũy thừa và số điểm mẫu lân cận tối ưu, sơ đồ độ sâu tại khu vực phía Nam vịnh Nha Trang được xây dựng bằng phần mềm mã nguồn mở QGIS trên lưới có độ phân giải cao 3 m x 3m (Hình 5). Từ sơ đồ phân bố không gian độ sâu cho thấy tại khu vực ven bờ của các đảo (Hòn Tằm, Hòn Miễu, Hòn Một, Hòn Tre, mặt phía bắc Hòn Mun) có độ sâu thấp hơn 15 m. Tại các khu vực nằm giữa các đảo, độ sâu thường lớn hơn 15 m, thuận lợi cho giao thông hàng hải tại khu vực phía Nam vịnh Nha Trang. Tại các vùng nước xung quanh Hòn Nọc và phía Nam Hòn Mun, độ sâu lớn hơn 25 m. Nhìn chung, độ sâu có xu hướng tăng từ bờ ra khơi, những khu vực có kinh độ lớn hơn 317500 thường có độ sâu lớn hơn 25 m. 

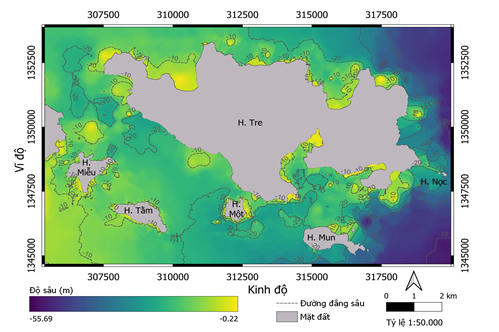
Hình 5. Sơ đồ độ sâu tại khu vực phía Nam vịnh Nha Trang với độ phân giải 3m

4. KẾT LUẬN VÀ KIẾN NGHỊ

         Dựa vào nguồn dữ liệu mở GEBCO_2023 kết hợp với dữ liệu độ sâu đo hiện trường, nghiên cứu đã tối ưu hóa tỷ lệ dữ liệu (80% dữ liệu huấn luyện và 20% dữ liệu kiểm định) và các tham số (tham số lũy thừa bằng 2 và số lượng điểm mẫu lân cận bằng 4) trên thuật toán nội suy IDW nhằm xây dựng sơ đồ độ sâu khu vực phía Nam vịnh Nha Trang. Sai số giữa dữ liệu độ sâu đo đạc và độ sâu dự báo từ mô hình IDW đạt 0,597 m.

          Phân bố không gian của độ sâu tại vùng nghiên cứu có xu hướng tăng từ bờ ra khơi. Sơ đồ độ sâu tại vùng nghiên cứu được sử dụng như dữ liệu đầu vào để xây dựng sơ đồ phân bố hệ sinh thái ngầm, là nguồn dữ liệu tham khảo có giá trị cho các nghiên cứu về lĩnh vực khoa học biển và giao thông hàng hải trên biển.

           Trong nghiên cứu này, dữ liệu độ sâu từ mô hình GEBCO_2023 được sử dụng để bổ sung cho các điểm đo đạc hiện trường, nhằm tránh tình trạng dữ liệu độ sâu thực tế bị phân cụm và không bao phủ đều khắp khu vực nghiên cứu. Tuy nhiên, trong các nghiên cứu khác, nếu dữ liệu độ sâu đo đạc hiện trường đủ lớn và bao phủ toàn bộ khu vực nghiên cứu, các nhà nghiên cứu nên ưu tiên sử dụng hoàn toàn dữ liệu này để thực hiện thuật toán nội suy không gian để đảm bảo độ chính xác cao hơn.

Lời cảm ơn: Nghiên cứu này nhận được sự hỗ trợ chuyên môn, kinh phí và là một phần của đề tài cấp Trung tâm Nhiệt đới Việt - Nga, mã số VB.Đ1.11/24.